Problem 64

Problem 64: Elastic band on cylinder ( $✓$ ) 2001 Paper I

A smooth cylinder with circular cross-section of radius $a$ is held with its axis horizontal. A light elastic band of unstretched length $2 π a$ and modulus of elasticity $λ$ is wrapped round the circumference of the cylinder, so that it forms a circle in a plane perpendicular to the axis of the cylinder. A particle of mass $m$ is then attached to the rubber band at its lowest point and released from rest.

(i): Given that the particle falls to a distance $2 a$ below the axis of the cylinder, but no further, show that $λ = \frac{9 π m g}{{(3 \sqrt{3} - π)}^{2}} .$
(ii): Given instead that the particle reaches its maximum speed at a distance $2 a$ below the axis of the cylinder, ﬁnd a similar expression for $λ$ .

Comments

This question uses the most basic ideas in mechanics, such as conservation of energy. I included it in this selection of questions without realising that the properties of stretched strings are not in the syllabus (which is given in the appendix). However, I didn’t throw it out: it is a nice question and the only two things you need to know about stretched strings are, for a stretched string of natural (i.e. unstretched) length $l$ and extended length $l + x$ with modulus of elasticity $λ$ :

the potential energy stored in the stretched string is $\frac{λ x^{2}}{2 l};$
the tension in the stretched string, by Hooke’s law, is $\frac{λ x}{l}$ .

Solution to problem 64

The diagram below shows the system when the particle has fallen a distance $a$ from its initial position.

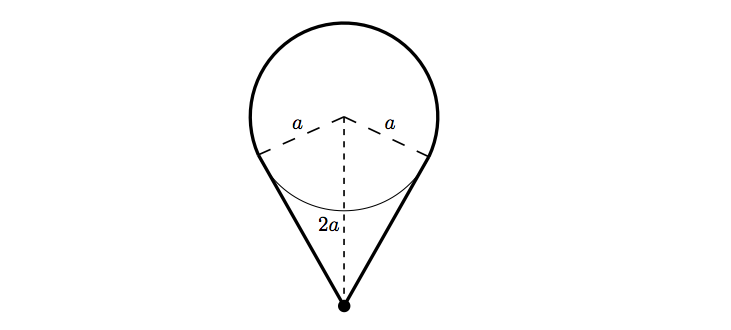
A bit of geometry (including Pythagoras) on the above diagram shows that the length of the extended band is $2 π a - 2 a arccos \frac{1}{2} + 2 \sqrt{3} a$ so the extension of the band is

- 2 a arccos \frac{1}{2} + 2 \sqrt{3} a, i.e. 2 a (\sqrt{3} - \frac{1}{3} π) .

(i) At the lowest point, the speed is zero. That suggests using an energy equation, which will involve speed and displacement (for the potential energy) but not acceleration.

Conserving energy (taking the initial potential energy to be zero), we ﬁnd that when the particle has fallen a distance $a$ and has speed $v$ ,

0 = \frac{1}{2} m v^{2} + \frac{1}{2} λ \frac{{[2 a (\sqrt{3} - \frac{1}{3} π)]}^{2}}{2 π a} - m g a .

At the lowest point, $v = 0$ , which gives the required answer.

(ii) Now we are interested in the point where the speed is greatest, i.e. where the acceleration is zero, so this time we should use the equation of motion of the particle.

The component of the tension $T$ in the band in the vertical direction, acting upwards on the particle, when the particle has fallen a distance $y$ is $2 T cos 𝜃$ where $sin 𝜃 = a ∕ (a + y)$ . Applying Newton’s second law to the motion of the particle gives

m ÿ = 2 T cos 𝜃 - m g,

(

*

)

where, by Hooke’s law, $T = λ \times extension ∕ 2 π a$ . At the maximum speed, $ÿ = 0$ . This occurs at $y = a$ , so $(*)$ becomes

0 = 2 λ \frac{2 a (\sqrt{3} - \frac{1}{3} π)}{2 π a} \frac{\sqrt{3}}{2} - m g .

In this case $λ = \frac{\sqrt{3} π m g}{3 \sqrt{3} - π}$ .

Post-mortem

The question was relatively simple because you only needed to evaluate energy or tension at very special points: maximum extension or maximum speed. You could of course have worked from the general equation of motion $(*)$ , with $cos 𝜃 = \sqrt{2 a y + y^{2}} ∕ (a + y)$ and extension $2 \sqrt{2 a y + y^{2}} - 2 a arcsin (a ∕ (a + y))$ , but you can’t solve the differential equation to ﬁnd the general motion. It would be possible for small oscillations.